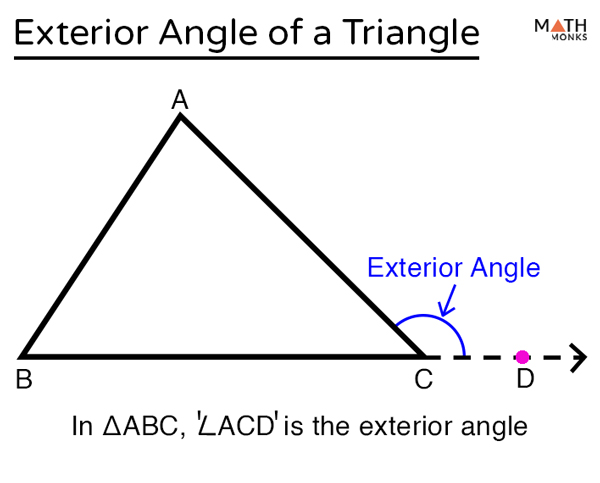
The exterior angle of a triangle is the angle formed between one side and the extension of its adjacent side.
Shown below is the ΔABC where ∠ACD is the exterior angle formed by the side AC and the extension of the side BC to D.

Every triangle has three exterior angles, two at each vertex.
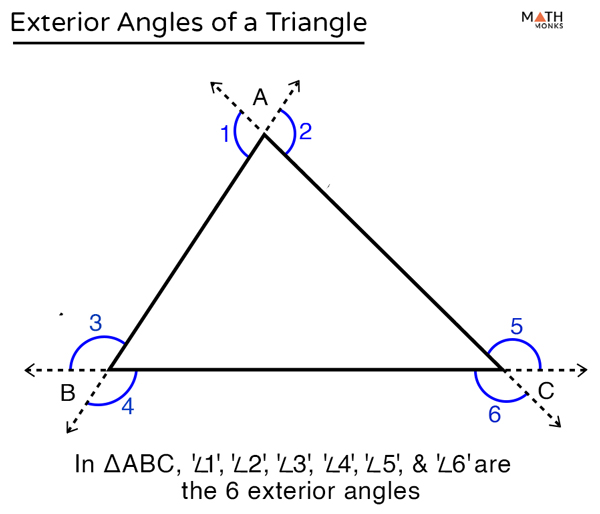
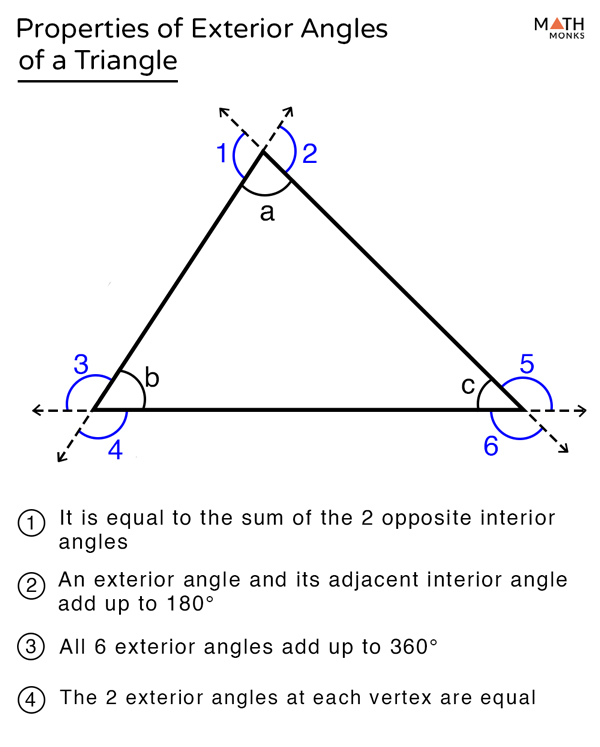

Prove Triangle Exterior Angle Theorem
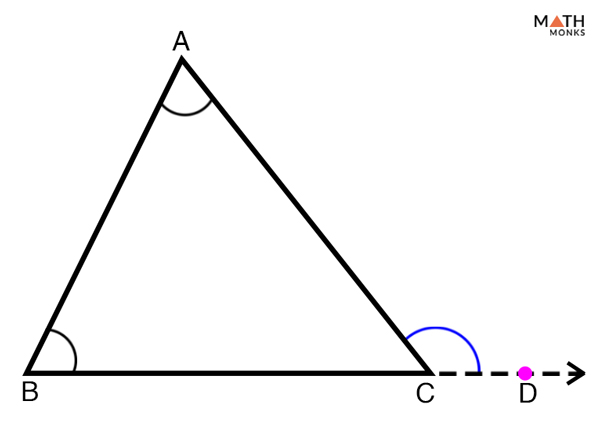
∠ACD = ∠ABC + ∠CAB
Given: ΔABC, ABD is a line segment
∠ACD + ∠BCA = 180° … (1) [∠ACD & ∠BCA form a linear pair, they are supplementary]
∠ABC + ∠BCA + ∠CAB = 180° …. (2) [Angle Sum Property of a Triangle]
Substituting (1) in (2), we get,
∠ACD + ∠BCA = ∠ABC + ∠BCA + ∠CAB
∠ACD = ∠ABC + ∠CAB
Hence Proved
Given below are some solved examples to understand the concept.
Here, we will apply the exterior angle theorem to find the missing interior or exterior angles in a triangle.
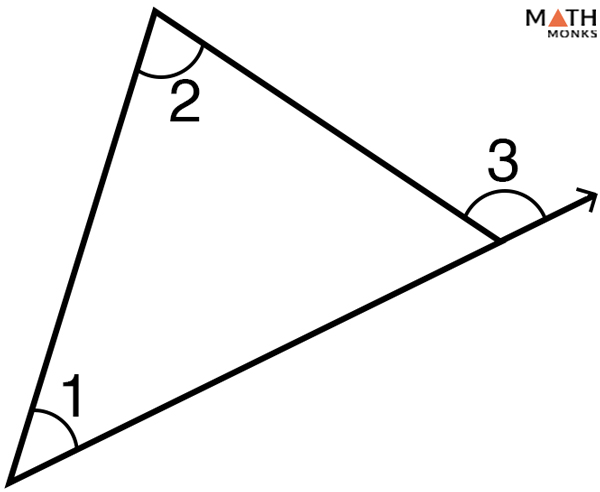
In the given triangle, if m∠1 = 40° and m∠2 = 80°, find m∠4.
As we know, from the exterior angle theorem,
m∠4 = m∠1 + m∠2, here m∠1 = 40°, m∠2 = 80°
m∠4 = 40° + 80° = 120°
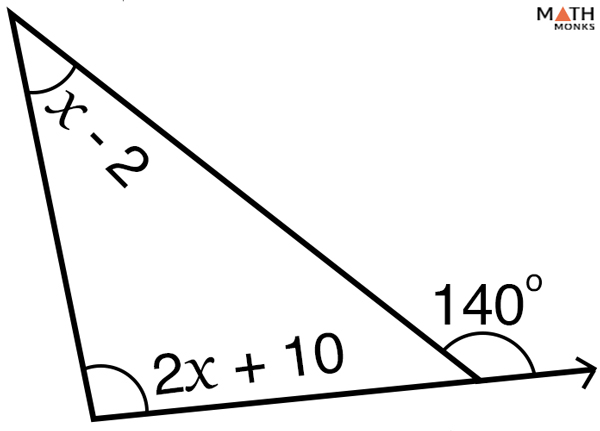
Solve for x.
As we know, from the exterior angle theorem,
(x – 2) + (2x + 10) = 140°
=> 3x + 8 = 140°
=> 3x = 132
=> x = 44
If the measure of the exterior angle is (5x – 10) degrees, and the measure of the two remote interior angles are 30 degrees and (x + 20) degrees, find x.
As we know, from the exterior angle theorem,
(5x – 10) = 30° + (x + 20)
5x – x = 30° + 20° + 10°
4x = 60°
x = 15°
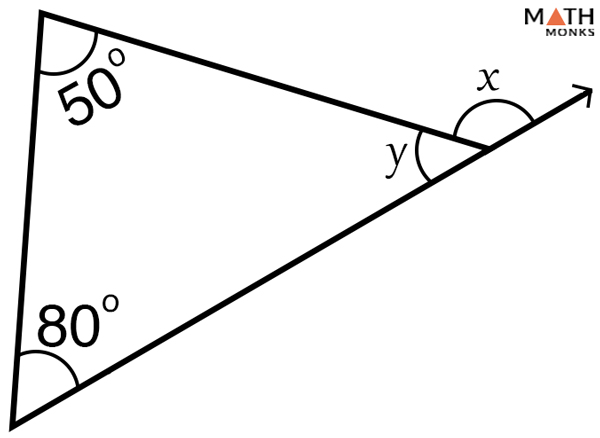
Calculate values of x and y in the given triangle.
In the given triangle, x is the exterior angle and y is the interior angle
As we know, from the exterior angle theorem,
x = 80° + 50° = 130°
Now, as x and y are linear pairs that add up to 180°
Thus,
x + y = 180°, here x = 130°
130° + y = 180°
y = 180° – 130° = 50°
Last modified on August 3rd, 2023